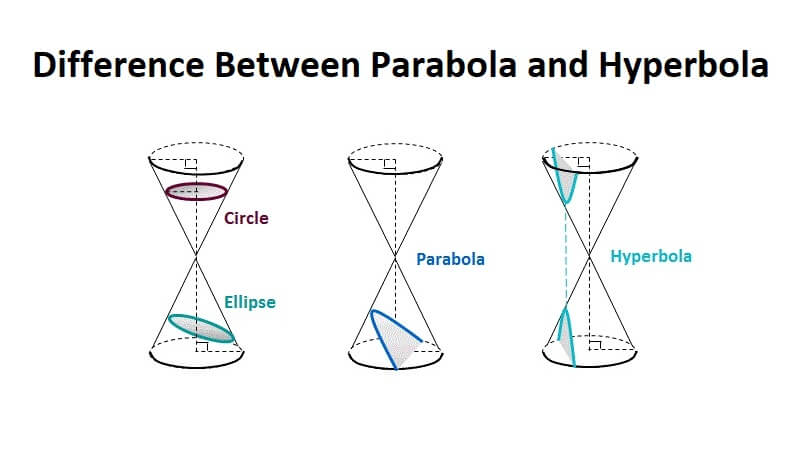
A conic section is a curve that is formed when a plane crosses a cone at a specified point on its axis. Ellipse, parabola, and hyperbola are the three forms of conic sections that may be found.
Essentially, an ellipse is a planar curve with two focus points that looks similar to a circle in shape. The parabola and hyperbola portions, on the other hand, are difficult to understand.
Parabola Vs. Hyperbola
When comparing a parabola with a hyperbola, the most significant distinction is that the former is composed of a single open curve with eccentricity one, whereas the latter has two curves with eccentricities larger than one.
A parabola is a single open curve that stretches indefinitely into the distance between points. One focus and one directrix are located on each side of the U-shaped structure.
A hyperbola is an open curve with two branches that are not linked to one another. This organization has two foci and two directrices, one for each branch of the organization.
What is Parabola?
It is the locus of all points that are equidistant between two points or two lines, which is represented by a parabola. This location is referred to as the focal point, and this line is referred to as the directrix.
When a plane meets a cone in a direction parallel (in the ideal situation) to the cone’s slant height, a parabola is produced.
The following is the general equation of a parabola:
y = ax2, where a = 0.
The form of the curve is determined by the value of the variable a.
If an is greater than zero, the parabola’s mouth expands to the top.
If the value of an is less than zero, the mouth of the parabola opens to the bottom.
The point of convergence of the preceding parabola is (0, 1/4a). The directrix is represented by (-1/4a).
When a=1, on the other hand, the parabola is referred to as a unit parabola.
An eccentricity of one is found in a parabola.
A parabola is circularly symmetric around its axis of rotation. The curves look like parallel lines when seen from an infinite distance.
What is Hyperbola?
It is the locus of all points that have a constant difference from two separate points, which is represented by a hyperbola. The hyperbola’s foci are the places at which the hyperbola intersects.
In the case of a solid plane intersecting a cone in a path that is parallel to the cone’s perpendicular height, a hyperbola is created.
According to this, the general equation of a hyperbola is
One is equal to (x-2)2/a2 – (y-2)2/b2
The foci of the hyperbola shown above are (a2+b2) sqrt(a2+b2) and (a2+b2).
The vertices are represented by (a, b).
In mathematics, a hyperbola is defined as having an eccentricity larger than one.
A hyperbola has two axes of symmetry that are parallel to each other. These are referred to as the transverse axis and the conjugate axis, respectively.
Difference Between a parabola and a hyperbola
- Conic sections are represented by the parabola and the hyperbola. They are all diverse in terms of form and features.
- A parabola is a locus that contains all of the points that are at equal distance from a focus and a directrix. 2. A hyperbola, on the other hand, is a locus that contains all of the locations for which the difference in distance between two foci is always the same.
- A parabola is an open curve with a single focus and directrix, but a hyperbola is an open curve with two branches and two foci and directrices, as shown in the diagram.
- A parabola has an eccentricity of one, while a hyperbola has an eccentricity of larger than one. 3.
- In the case of a plane intersecting a cone at its slant height, a parabola is produced. A hyperbola, on the other hand, is generated when a plane crosses a cone along with the height of the cone’s perpendicular axis.
- The equation for a parabola is y = ax2 (y = ax2 = ax2). On the other hand, the equation for a hyperbola is x2/a2 – y2/b2 = 1, which is the same as the equation for a parabola.
Conclusion
Conic sections are made up of ellipses, paraboles, and hyperboles, among other shapes. Due to the fact that they are formed by the intersection of a cone and a plane, conic sections are often referred to as such. Parabolas are a single endless curve that may be drawn in any direction. They are the collection of points that are equally spaced apart from the focus and directrix.
Hyperbolas are curves with two branches, as the name implies. Essentially, they are the locus of points that are separated by a constant distance between two foci. The distinction between them is based on their peculiarities. Parabolas have an eccentricity of one, but hyperbolas have an eccentricity larger than one, as seen in the diagram below.
In real life, parabolas may be used in a variety of ways. Architectural and technical applications, spaceship design, reflectors, and holographic materials are all examples of how they are employed. Hyperbolas are widely used in a variety of fields, including radio engineering, satellite design, optics, computers, and solar clocks. In actuality, our cosmos is shaped like a hyperbola, as seen below.